The height of the geostationary orbit is 35786 kilometers above earth in geostationary orbit the satellite moves with an orbital speed of 11068 km per hours.
Calculate the orbital height of a geostationary satellite.
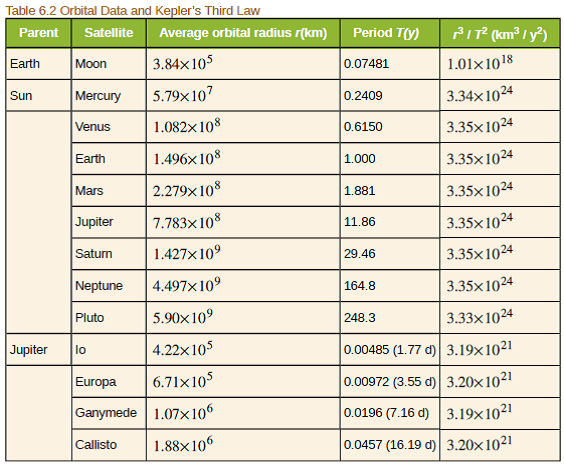
P is the orbital period.
Speed of a satellite in circular orbit orbital velocity period centripetal force physics problem duration.
Through the use of re arranging the above equation we can come to the equation.
A minimum of three satellites are needed to cover the entire earth super synchronous orbit is a disposal storage orbit above gso.
The organic chemistry tutor 143 911 views 17 18.
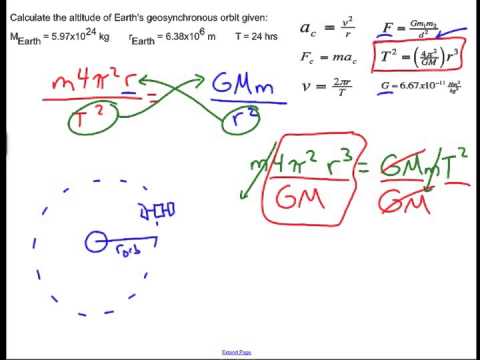
Mission control wishes to place a satellite in circular orbit above the earth.
R orbital radius earth s equatorial radius height of the satellite above the earth surface r 6 378 km 35 780 km r 42 158 km r 4 2158 x 107 m speed.
B calculate the height at which the satellite orbits above the surface of the earth.
The period of a satellite is the time it takes.
An object in such an orbit has an orbital period equal to the earth s rotational period one sidereal day and so to ground observers it appears motionless in a fixed.
The satellite must have a period.
An object s orbital altitude can be computed from its orbital period and the mass of the body it orbits using the following formula.
To calculate the radius of a geostationary orbit the centripetal force must equal the gravitational force on the satellite or mass.
A geostationary orbit also referred to as a geosynchronous equatorial orbit geo is a circular geosynchronous orbit 35 786 kilometres 22 236 miles above earth s equator and following the direction of earth s rotation.
From earth they would seem drifting in westerly direction.
H is the altitude height of the object.
When a satellite travels in a geosynchronous orbit around the earth it needs to travel at a certain orbiting radius and period to maintain this orbit.
The radius of the earth is 6400km and its mass is 6x10 24 kg.
H 4 22 10 7 6 37 10 6 3 583 10 7 m.
From the relationship f centripetal f centrifugal we note that the mass of the satellite m s appears on both sides geostationary orbit is independent of the mass of the satellite.
R g m2 t 4π we know that m2 is the mass of the earth at 5 98 10 24 kg t is the time period and g the universal gravitation constant at 6 67 x10 11 kg 2.
G is the gravitational constant.
A a geostationary orbit is when the satellite remains vertically above the same point on the equator at all all times and consequently has an orbital period of 24 hours.